Edwards Soft Shackle Tying
Pass one end through the center and make two marks. Pass the long end through the short at the first mark. Thread the short end along inside the long one to exit at the second mark and tighten. Pass the long end through the short. Lay out the two ends to tie the Lanyard Knot.

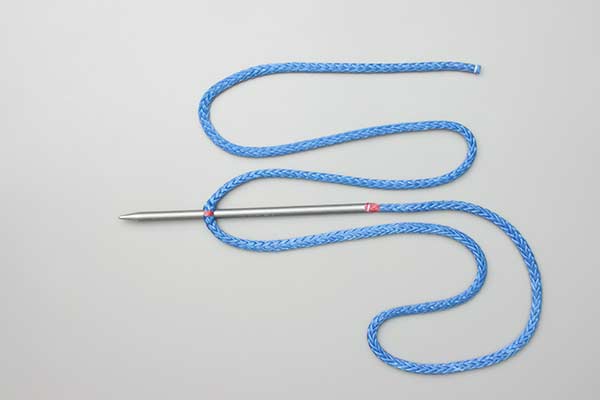























Better (Edwards) Soft Shackle Details
// Soft Shackle Edwards function Calculate(obj) // Calculate from Rope Dia and Shackle Dia { diam = parseFloat(obj.diam.value); // Rope Dia intdiam = parseFloat(obj.idia.value); // Internal Shackle diam stretch = 1.2; // Stretch for 1/4" and up if (diam == .109) stretch = 1.1875; if (diam == .125) stretch = 1.23; if (diam == .15625) stretch = 1.23; if (diam == .1875) stretch = 1.21538; shack = 3.14159 * intdiam + 10.272385 * diam; // Shackle Length body = (intdiam + 1.5 * diam) * 3.1416; // Length less knot totalrope = (112*diam + (1 + stretch)*(intdiam + 1.5*diam) * 3.14159); // Total Line Length mark1 = 16 * diam; mark2 = 16*diam + stretch*((intdiam + 1.5*diam)*3.14159 - 13.11*diam) ; // Exit Point capacity = (intdiam - 1.9099 * diam); obj.shack.value = "" . concat(Math.round(10 * shack) / 10," in"); // Shackle Length obj.length.value= "" . concat(Math.round(10 * totalrope) / 10," in"); // Total Line Length obj.mark1.value = "" . concat(Math.round(10 * mark1) / 10," in"); // First Crossover obj.mark2.value = "" . concat(Math.round(10 * mark2) / 10," in"); // Exit Point obj.idia2.value = "" . concat(Math.round(10 * capacity) / 10," in"); // Capacity } function Calculatemetric(obj) // Calculate from Rope Dia and Shackle Dia { diammetric = parseFloat(obj.diammetric.value); // Rope Dia intdiammetric = parseFloat(obj.idiametric.value); // Internal Shackle diam stretchmetric = 1.2; // Stretch for 6mm and up if (diammetric == 2) stretchmetric = 1.1875; if (diammetric == 3) stretchmetric = 1.23; if (diammetric == 4) stretchmetric = 1.23; if (diammetric == 5) stretchmetric = 1.21538; shackmetric = 3.14159 * intdiammetric + 10.272385 * diammetric; // Shackle Length bodymetric = (intdiammetric + 1.5 * diammetric) * 3.1416; // Length less knot totalropemetric = (112*diammetric+(1+stretchmetric)*(intdiammetric+1.5*diammetric)*3.14159); // Total Line Length mark1metric = 16 * diammetric; mark2metric = 16*diammetric+stretchmetric*((intdiammetric+1.5*diammetric)*3.14159-13.11*diammetric); // Exit Point capacitymetric = (intdiammetric - 1.9099 * diammetric); // Maximum capacity obj.shackmetric.value = "" . concat(Math.round(shackmetric) / 10," cm"); // Shackle Length obj.lengthmetric.value= "" . concat(Math.round(0.1 * (totalropemetric))," cm"); // Total Line Length obj.mark1metric.value = "" . concat(Math.round(16 * diammetric) / 10," cm"); // First Crossover obj.mark2metric.value = "" . concat(Math.round(mark2metric) / 10," cm"); // Exit Point obj.idia2metric.value = "" . concat(Math.round(capacitymetric) / 10," cm"); // Capacity } .tablecellinputleft, .tablecellinputright, .tablecellcenter { /* ## Soft Shackle Edwards */ font-size: 12px; border-style: solid; border-width: 1px; border-color: #000000; } .tablecellinputleft { /* ## Soft Shackle Edwards */ background-color: #0000FF; padding: 1px 3px 1px 3px; } .tablecellinputright { /* ## Soft Shackle Edwards */ background-color: #FF0000; padding: 1px 3px 1px 3px; } .tablecellcenter { /* ## Soft Shackle Edwards */ background-color: #EEEEEE; padding: 5px 3px 1px 3px; text-align: center; }Purpose: A Soft Shackle offers a strong lightweight alternative to a metal shackle.
Name: A Better Soft Shackle was proposed by Allen Edwards, the originator of this design and Webmaster of L-36.com.
Alternative: The commoner Soft Shackle is made with the lines running inside each other – elegant but may be harder to release. The Kohlhoff Shackle has the loop composed of two lines all the way around.
Technique: Edwards provides detailed written instructions on his page. He also emphasizes that final tightening of the Lanyard (Diamond) Knot is critical. He passes the two tails through a hole in a metal bar and exerts traction using vice-grip pliers – look near the bottom of: Better Soft Shackle page. The tightened knot should feel like a wooden ball and, if not extremely tight, Edwards warns it may slip.
Lengths Needed: The Edwards Calculator bases the lengths required on the shackle length. The calculator below is based on the finished inner diameter and allows input in either English or Metric units. First enter the size of the finished shackle diameter and then the rope diameter and press the adjacent Calculate button. Measurements for are taken from the tip of the small loop (Red marks in Frame 4).
| English | Metric | |
| in | Inner Diameter (D) | mm |
| 7/64 in 1/8 in 5/32 in 3/16 in 1/4 in 5/16 in 3/8 in 7/16 in 1/2 in 9/16 in 5/8 in | Diameter of the Rope | 2 mm 3 mm 4 mm 5 mm 6 mm 7 mm 8 mm 9 mm 10 mm 11 mm 12 mm 14 mm 16 mm |
| Rope Length Required | ||
| First Crossover from End | ||
| Exit of Bury from End | ||
| Usable Inner Diameter | ||
| Shackle Length (L) |
The Usable Inner Diameter is somewhat smaller than the Inner Diameter (D) because the process of closing the shackle takes up some of the line. (Note: the calculation is derived from Edwards method and the results are similar).
To calculate these values manually, first calculate S (Stretch):
-
If D = 7/64" (or 2mm), S = 1.1875
If D = 1/8" (or 3mm), S = 1.23
If D = 5/32" (or 4mm), S = 1.23
If D = 3/16" (or 5mm), S = 1.21538
Otherwise S = 1.2
Where
-
R = Rope diameter, e.g., 0.25",
D = Intended Diameter of Shackle, e.g., 2":
Then:
-
Rope Length required =112 x R + (1 + S) x (D + 1.5 x R) x 3.1416
Mark 1 = 16 x R
Mark 2 = 16 x R + S x ((D + 1.5 x R) x 3.14159 - 13.11 x R)
Maximum Load Diameter = D - 1.9099 x R
Shackle Length (tip to beneath knot) = 3.1416 x D + 10.272 x R
Tail Lengths: If the knot has been adequately tightened, trim the tails to about 1/4" long. If not really tight, then leave at least an inch.
Use: The completed shackle provides an excellent way of attaching two jib sheets to the jib – see photo on right courtesy of Allen Edwards. Here Edwards uses a Velcro Strap to keep the Lanyard Knot centered in the ring and out of the way of the rigging.
Advantages: The soft shackle weighs little and is less likely to cause injury it strikes a crew member. The array of soft shackle and jib sheets pulls across in front of a mast with little tendency to catch - reducing the need to place a crew member up on the foredeck. This version is easier to release than the more common Soft Shackle.
Strength: Soft shackles have been extensively tested. The ideal strength might approach four times the line strength as there are two lines on each side of the shackle – four in all. In practice, the line just under the knot and the kinking in the loop are the weak points and Evans Starzinger has shown that breakage typically occurs around 175% of Line Strength. This means when attached to a jib sheet using similar rope, the sheet will part first – not the soft shackle.



